728x90
트리
시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
| 2 초 | 128 MB | 40684 | 11357 | 8730 | 27.976% |
문제
트리에서 리프 노드란, 자식의 개수가 0인 노드를 말한다.
트리가 주어졌을 때, 노드 하나를 지울 것이다. 그 때, 남은 트리에서 리프 노드의 개수를 구하는 프로그램을 작성하시오. 노드를 지우면 그 노드와 노드의 모든 자손이 트리에서 제거된다.
예를 들어, 다음과 같은 트리가 있다고 하자.

현재 리프 노드의 개수는 3개이다. (초록색 색칠된 노드) 이때, 1번을 지우면, 다음과 같이 변한다. 검정색으로 색칠된 노드가 트리에서 제거된 노드이다.
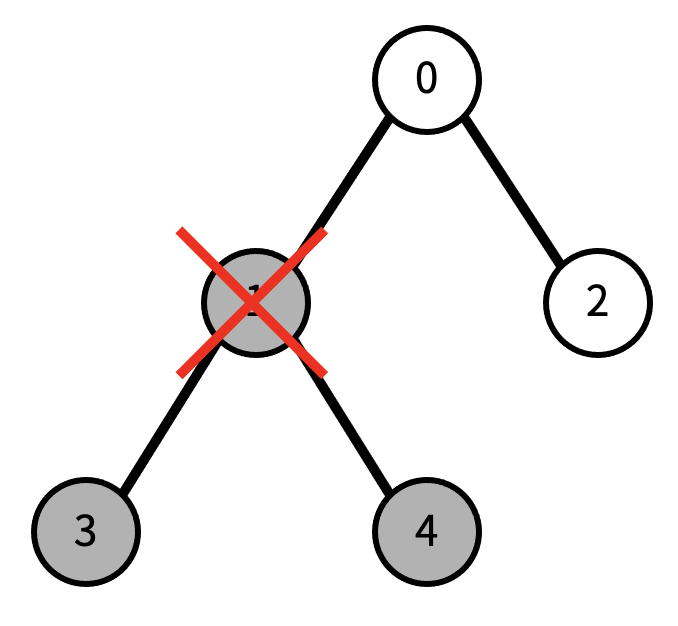
이제 리프 노드의 개수는 1개이다.
입력
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다. 셋째 줄에는 지울 노드의 번호가 주어진다.
출력
첫째 줄에 입력으로 주어진 트리에서 입력으로 주어진 노드를 지웠을 때, 리프 노드의 개수를 출력한다.
예제 입력 1 복사
5
-1 0 0 1 1
2
예제 출력 1 복사
2
예제 입력 2 복사
5
-1 0 0 1 1
1
예제 출력 2 복사
1
예제 입력 3 복사
5
-1 0 0 1 1
0
예제 출력 3 복사
0
예제 입력 4 복사
9
-1 0 0 2 2 4 4 6 6
4
예제 출력 4 복사
2
흐름

코드
#include <bits/stdc++.h>
using namespace std;
int n, a[50], d, ret;
set<int> s; //리프노드가 아닌 노드 번호 저장
//삭제 노드를 부모로 하는 노드를 차례대로 지우기(dfs)
void dfs(int d){
for(int i=0;i<n;i++){
if(a[i]==d) { //삭제노드를 부모노드로 한다면
dfs(i); //자식인 리프노드(삭제노드가 조상노드)까지 내려가기
a[i]=-2; //올라가며 삭제 표시
}
}
}
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
//1. 입력받기
cin >> n;
for(int i=0;i<n;i++){
cin >> a[i];
}
cin >> d;
//2-1. 삭제노드의 부모 노드 -2으로 표시
a[d]=-2;
//2-2. dfs 수행(삭제 노드를 부모로 하는 노드 차례대로 삭제(-2로) 표시)
dfs(d);
//3. 리프노드 세기
for(int i=0;i<n;i++){
if(a[i] == -2) s.insert(i); //삭제된 노드는 리프노드 아님(삭제된 노드 저장)
else if(a[i]==-1) continue; //-1은 노드 번호가 아닌 단지 루트노드 나타내기 위한 것
else s.insert(a[i]); //부모 노드 저장, 중복을 없애기 위해 세트 사용
}
//4. 리프노드 수 계산하기 : 전체 노드 수 - (삭제된 노드 수 + 삭제 과정 이후의 부모 노드 수)
ret = n- s.size();
// 정답 출력하기
cout << ret << "\n";
return 0;
}
코드 추가 설명
- 삭제된 노드는 부모 노드를 저장하는 배열에 -2로 저장했다. (원래 부모였던 노드가 자식 노드가 다 삭제되어 리프노드가 될 수 있다.)
- 리프 노드가 아닌 노드부터 구한 이유는 부모 노드로 언급된 노드를 저장하여 전체 노드에서 제외할 필요성이 있기 때문이다.
리프 노드 = 초기의 전체 노드 수 - (삭제 과정 이후의 부모 노드 + 삭제된 노드)
노드를 삭제할때 삭제 표시를 하는 방법과 순회를 못하게 막는 2가지 방법이 있다.
전자가 내가 푼 방법이고, 선생님은 두번째 방법으로 설명하셨다.
팁
- 트리 구조는 루트 노드부터 탐색을 시작하자.(한번에 탐색 가능)
- 벡터에 adj[부모]={자식1, 자식2...} 이런 구조로 저장하면 dfs 한번에 탐색할 수 있다.
선생님 코드
#include <bits/stdc++.h>
using namespace std;
int n,r,temp,root;
vector<int> adj[54];
int dfs(int here){
int ret = 0;
int child = 0;
for(int there:adj[here]){ //자식 노드 하나씩 꺼냄
if(there == r) continue; //삭제할 노드이면 탐색 안함
ret += dfs(there);
child++;
}
if(child==0) return 1; //리프 노드
return ret;
}
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
//1. 입력받기
cin >> n;
for(int i=0;i<n;i++){
cin >> temp; //부모 입력받음
if(temp == -1) root = i;
else adj[temp].push_back(i); //adj[부모]={자식1,자식2..}
}
cin >> r; //삭제 노드
if(r==root){
cout << 0 << "\n";
return 0;
}
//dfs
cout << dfs(root) << "\n";
return 0;
}
리프노드까지 가서 +1씩 하는 방법이다.
벡터에 없는 원소를 접근할 시에는 동작이 수행되지 않는다. (size() 등등)
위 코드는 외워서 트리 문제일때 활용할 수 있도록 해야겠다.
728x90
