728x90
url : https://www.acmicpc.net/problem/11051
11051번: 이항 계수 2
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 1,000, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
이항 계수 2 문제이다.
N이 1000 이하인 이항 계수에 10007로 나눈 나머지를 구하는 문제이다.
수학적 지식을 이용해야 빡센 시간 복잡도를 통과할 수 있다.
이항 계수 계산
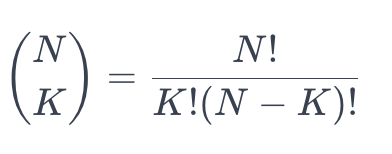
이항 계수는 팩토리얼 계산을 베이스로 한다.
N이 커질수록 직접 N!, K!, (N-K)!를 구하여 나누는 것은 매우 큰 수가 되기 때문에, 어떤 타입이던 오버플로우가 발생한다.
참고로 13!부터 int 타입 범위를 초과하고, 21!부터 long long 타입 범위를 초과한다.
그러므로 이항계수의 값을 구해 (각각의 팩토리얼 계산의 결과값을 구해서) 10007로 나눌 생각을 하지 말고,
이항계수를 구하는 과정에서 단계별 계산된 값에 대해 10007을 계속해서 나누어야한다.
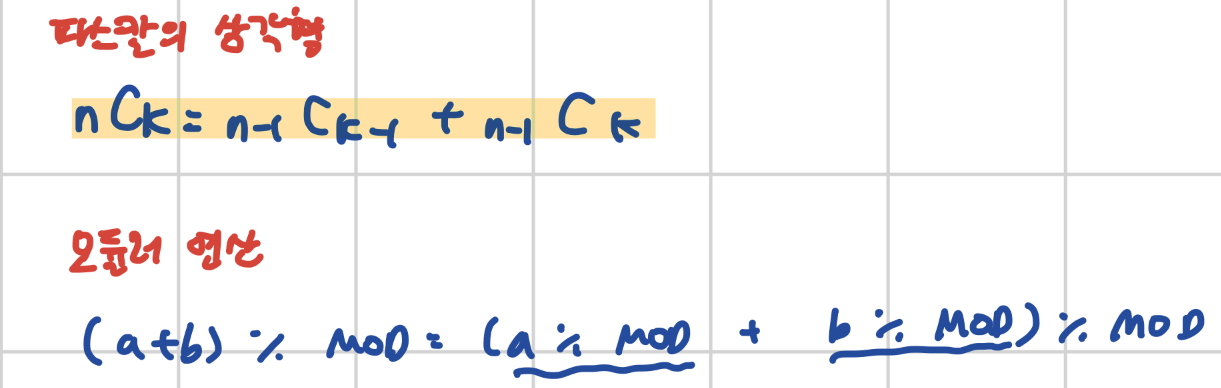
파스칼의 삼각형 공식을 이용하여 이항 계수를 단계별로 구할 수 있다.
단계별로 구하면서 결과값을 MOD로 나누므로써 오버플로우를 방지한다.
파스칼의 삼각형 공식을 모듈러 연산 공식에 적용하면 다음과 같다.

코드로는 다음과 같다.
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
dp[i][j] = (dp[i-1][j-1]+dp[i-1][j]) % MOD;
}
}
정답 코드
#include <bits/stdc++.h>
using namespace std;
int n, k;
int dp[1004][1004];
const int MOD = 10007;
int main(){
//1. 입력받기
cin >> n >> k;
//2. dp 값 구하기
for (int i=1;i<=n;i++){
dp[i][0]=1;
dp[i][i]=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
dp[i][j] = (dp[i-1][j-1]+dp[i-1][j]) % MOD;
}
}
//3. 정답 출력
cout << dp[n][k] << "\n";
}

728x90
'알고리즘 > 알고리즘 문제풀이' 카테고리의 다른 글
| [프로그래머스] 181187: 두 원 사이의 정수 쌍 (2) | 2024.01.02 |
|---|---|
| [백준] 11401 : 이항 계수 3 (0) | 2023.12.31 |
| [백준] 11050 : 이항 계수 1 (2) | 2023.12.29 |
| [백준] 1655 : 가운데를 말해요, 정렬(우선순위 큐) (2) | 2023.12.28 |
| [백준] 12865 : 평범한 배낭, 0/1 배낭문제 (2) | 2023.12.27 |
