728x90
다익스트라 알고리즘
최단 경로 알고리즘 중 하나
출발점에서 다른 모든 노드로의 최단 경로를 구할 수 있다.
간선에 음의 가중치가 없어야한다.
알고리즘 복잡도 : O(ElogV)
코드
import java.util.ArrayList;
import java.util.PriorityQueue;
public class Main2 {
static class Node {
int to;
int weight;
public Node(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
public static void dijkstra(int v, int[][] data, int start) {
ArrayList<ArrayList<Node>> graph = new ArrayList<>();
for (int i = 0; i < v + 1; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < data.length; i++) {
graph.get(data[i][0]).add(new Node(data[i][1], data[i][2]));
}
int[] dist = new int[v + 1];
for (int i = 1; i < v + 1; i++) {
dist[i] = Integer.MAX_VALUE;
}
dist[start] = 0;
PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.offer(new Node(start, 0));
while (!pq.isEmpty()) {
Node curNode = pq.poll();
if (dist[curNode.to] < curNode.weight) {
continue;
}
for (int i = 0; i < graph.get(curNode.to).size(); i++) {
Node adjNode = graph.get(curNode.to).get(i);
if (dist[adjNode.to] > curNode.weight + adjNode.weight) {
dist[adjNode.to] = curNode.weight + adjNode.weight;
pq.offer(new Node(adjNode.to, dist[adjNode.to]));
}
}
}
for (int i = 0; i < v + 1; i++) {
if (dist[i] == Integer.MAX_VALUE) {
System.out.print("INF");
} else {
System.out.print(dist[i] + " ");
}
}
System.out.println();
}
public static void main(String[] args) {
// Test code
int[][] data = {{1, 2, 2}, {1, 3, 3}, {2, 3, 4}, {2, 4, 5}, {3, 4, 6}, {5, 1, 1}};
dijkstra(5, data, 1);
}
}
음의 간선이 포함된 그래프의 경우 최단 경로를 찾지 못하는 이유
다익스트라 알고리즘은 각 정점까지의 최단 경로를 찾을 때, 그 경로에 포함된 모든 이전 정점들의 최단 경로가 이미 확정되었다고 가정한다. 즉, 한번 확정된 최단 거리는 이후에 바뀌지 않는다고 가정한다.(한번씩만 계산)
하지만 음의 가중치가 존재할 경우, 음의 가중치 간선을 지나 이동하면 최단 거리가 더 짧은 경로를 새롭게 발견할 수 있다.
하지만 다익스트라는 각 정점까지의 최단 경로를 한번씩만 계산하므로 음의 간선이 존재하는 그래프의 경우 최단 경로를 잘못 구할 수 있다.
예시
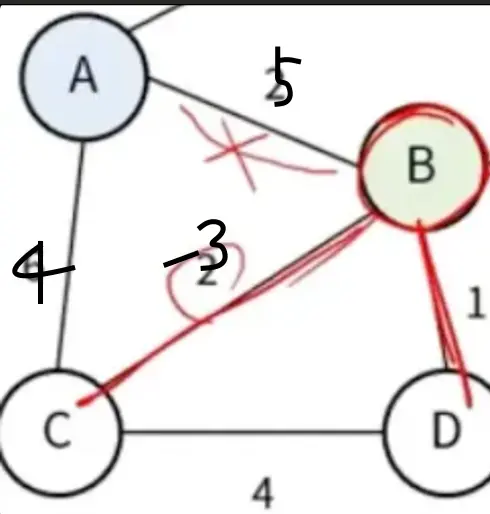
시작점 : A, 종료지점 : D
A
A에서 시작하여 B까지의 최단거리는 5, C까지의 최단거리는 4로 결정
C(C가 가장 A와 가까우므로)
A에서 시작하여 C를 거친 거리를 확인해보면 B는 1, D는 8
D(종료지점)
A에서 시작하여 B를 거쳐 D를 도착한 거리는 6
A에서 시작하여 C를 거쳐 D를 도착한 거리는 8
하지만 최단거리는 : 2 (A->C->B->D)
이유 : A->B의 최단거리를 처음부터 결정해버렸으므로 음수 가중치가 존재할 경우 새로 발견한 최단거리(A->C->B)로 경로를 업데이트할 수 없다.
결론 : 다익스트라 알고리즘에서는 음수 간선이 존재할 경우 최단 경로를 찾을 수 없다. 플로이드-워셜이나 벨만포드를 이용하자.
728x90
'알고리즘' 카테고리의 다른 글
| [PCCE 기출문제] 9번 / 이웃한 칸 (0) | 2023.11.24 |
|---|---|
| [프로그래머스] PCCP 기출문제 1번 : 붕대 감기 (0) | 2023.11.24 |
| 알고리즘 문제를 풀 때 순서 (0) | 2023.01.05 |
