[데이터베이스] 정규화 (이상현상, 함수 종속성, 무손실 분해)

이상현상

이상현상 : 테이블에 투플을 삽입할때 부득이하게 NULL 값이 입력되거나, 삭제시 연쇄삭제 현상이 발생하거나, 수정시 데이터의 일관성이 훼손되는 현상을 말한다.

잘못 설계된 테이블로 삽입, 삭제, 수정 같은 데이터 조작을 하면 이상현상이 일어난다.

조회시에는 이상현상이 일어나지 않는다.

 

이상현상의 종류

데이터베이스 설계가 잘못되면 이상현상, 즉 SQL문의 결과가 틀리거나 원하는 결과가 나오지 않는 등의 문제가 발생한다.

예시 테이블

CREATE TABLE Summer
(sid INTEGER,
class VARCHAR(20),
price INTEGER
);

학생번호, 수업명, 수업료 => 학생정보와 수업 정보가 함께 저장된다.

설계가 잘못된 테이블이다.

 

삽입 이상

투플 삽입 시 특정 속성에 해당하는 값이 없어 NULL값을 입력해야 하는 현상

NULL 값은 특별히 처리되므로 문제가 발생할 수 있다.

NULL + 3 = NULL 이며,
전체 조회(*)시 값이 세어지지만, 컬럼에 대해 count시 NULL은 세지 않는 문제가 있다.

select * from 학생수강 => 6
select count(강좌이름) from 학생수강 => 5

ex) 학생 정보 입력시 입력하지 않은 값에 대해서 NULL 값 입력

 

계절학기에 새로운 자바 강좌를 개설 => 삽입 이상

/* JAVA 강좌 삽입 */
INSERT INTO Summer VALUES(NULL, 'JAVA', 25000);

/* Summer 테이블 조회 */
SELECT * 
FROM SUMMER;

/* 투플 5개 */
SELECT COUNT(*) "수강인원"
FROM Summer;

/* sid의 수를 셀 경우 NULL은 세지 않아 결과는 4 */
SELECT COUNT(sid) "수강인원"
FROM Summer;

SELECT COUNT(*) "수강인원"
FROM Summer
WHERE SID is NOT NULL;

컬럼값이 NULL일 경우 해당 컬럼으로 count 쿼리시 NULL 제외하여 센다.

 

수정 이상

투플 수정시 중복된 데이터의 일부만 수정되어 데이터의 불일치 문제가 일어나는 현상
ex) 학생의 주소가 바뀌었는데 일부 테이블에만 그 값이 업데이트되는 경우

 

정상케이스 : FORTRAN 강좌의 수강료를 20000원에서 15000원으로 수정

/* FORTRAN 강좌 수강료 수정 */
UPDATE Summer
SET price=15000
WHERE class='FORTRAN';

SELECT * 
FROM Summer;

SELECT DISTINCT price "FORTRAN 수강료"
FROM Summer
WHERE class='FORTRAN';

 

수정 이상 발생 케이스 : FORTRAN 강좌의 수강료를 20000원에서 15000원으로 수정

/* 데이터 불일치 문제 발생 : FORTRAN 수업료가 한건만 수정된다. */
UPDATE Summer
set price=15000
WHERE class = 'FORTRAN' AND sid=100;

SELECT price "FORTRAN 수강료"
FROM Summer
WHERE class = 'FORTRAN';

모든 포트란 수업의 수업료가 갱신되지 않았다.

 

삭제 이상

투플 삭제 시 같이 저장된 다른 정보까지 연쇄적으로 삭제되는 현상이다.
ex) 수강 취소하여 delete문으로 수강신청 테이블의 투플을 삭제하였는데 학생 정보까지 함께 삭제

 

200번 학생의 계절학기 수강신청 취소 => 삭제 이상

/* 수강료 조회 */
SELECT price
FROM Summer
WHERE Class='C';

/* 200번 학생 수강신청 취소 */
DELETE
FROM Summer
WHRE sid=200;

/* C 강좌 수강료 조회 */
SELECT price "C 수강료"
FROM Summer
WHERE class='C';

학생이 수강취소를 하여 C 수업을 아무도 듣지 않는다.
그러므로 테이블에서 C 수업에 대한 수강료를 조회할 수 없다.

 

이상현상 해결

테이블의 구조를 수정하여 이상현상이 발생하지 않도록 하자.

 

=> Summer 테이블을 SummerPrice(과목, 수강료), SummerEnroll(학생) 테이블로 분리하였다.

 

이상현상은 두가지의 정보가 한 릴레이션에 저장되어 있기 때문에 발생한다.

 

삽입 이상 해결

과목과 수강료를 입력할 때 아직 학생이 신청하지 않았더라도 NULL 입력하지 않고 SummerPrice에 저장하면 된다.

수정 이상 해결

과목의 수강료를 수정하더라도 과목의 수강료는 SummerPrice 한 테이블에 모아 저장되므로 모든 데이터가 갱신될지에 대한 데이터 불일치 문제를 걱정하지 않아도 된다.

삭제 이상 해결

학생이 수강신청을 취소하더라도 SummerEnroll의 투플만 삭제되므로 과목에 대한 수강료 정보(SummerPrice)는 삭제되지 않는다.

 

함수 종속성

이상현상이 발생하는 테이블을 정상으로 만드려면 다시 테이블을 설계해야한다.

 

정규화

테이블 설계를 수정하여 정상으로 만드는 과정

정규화를 하기 위해서는 먼저 테이블을 분석하여 기본키와 함수 종속성을 판단해야 한다.

 

함수 종속성

함수 종속성: 테이블을 구성하는 속성 간에 의존 관계

정규화는 함수 종속성, 즉 테이블에 존재하는 여러 속성간의 의존관계를 정리하는 과정이다.

 

속성 B는 속성 A에 종속한다

속성 A의 값을 알면 다른 속성 B의 값이 유일하게 정해지는 의존 관계
A-> B : A는 B의 결정자, B는 종속 속성

 

학생번호 -> 학생 이름
학생번호 -> 주소
학과 -> 학과사무실
강좌이름 -> 강의실
(학생번호, 강좌이름) -> 성적

 

종속되어보이지만 그렇지 않은 경우

학생이름 -> 학과

동명이인이 있을 수 있기 때문이다.

 

함수 종속성을 판단할때는 릴레이션의 현재 인스턴스만을 보고 판단하는 것이 아닌 속성이 갖는 의미를 가지고 판단해야한다.

 

왼쪽 속성의 모든 값에 의해 오른쪽 속성의 값이 유일하게 결정될 때 함수적으로 종속한다라고 한다.
릴레이션의 속성간에 함수적으로 종속하는 성질을 함수 종속성이라고 한다.

 

함수 종속성 다이어그램

함수 종속성을 나타내는 표기법이다.
릴레이션의 속성을 직사각형으로, 속성 간의 함수 종속성을 화살표로 나타낸다.
복합속성의 경우 직사각형으로 묶어서 그린다.

함수 종속성 규칙

릴레이션에 존재하는 모든 종속관계{X->Y, ...}를 구하면 이 집합으로부터 유도할 수 있는 종속관계가 있다.

 

적용 예시

 

함수 종속성과 기본키

릴레이션 R(K, A1, A2, ..., An)에서 K가 기본키면 K->R이 성립한다. 즉, 기본키는 릴레이션의 모든 속성에 대해 결정자이다.
릴레이션이 R(K, A, B, C)일때, 기본키값은 유일하므로 K-> A, K->B, K->C이다.
함수 종속성 규칙(결합 규칙)을 적용하면 K->ABC, 즉 K->R이다.

 

이상현상과 결정자

이상현상은 한 개의 릴레이션에 두 개 이상의 정보가 포함되어 있을 때 나타난다.
이 전 테이블에서도 학생 정보와 강좌 정보가 한 릴레이션에 포함되어 있기 때문에 이상현상이 일어난다.

 

 

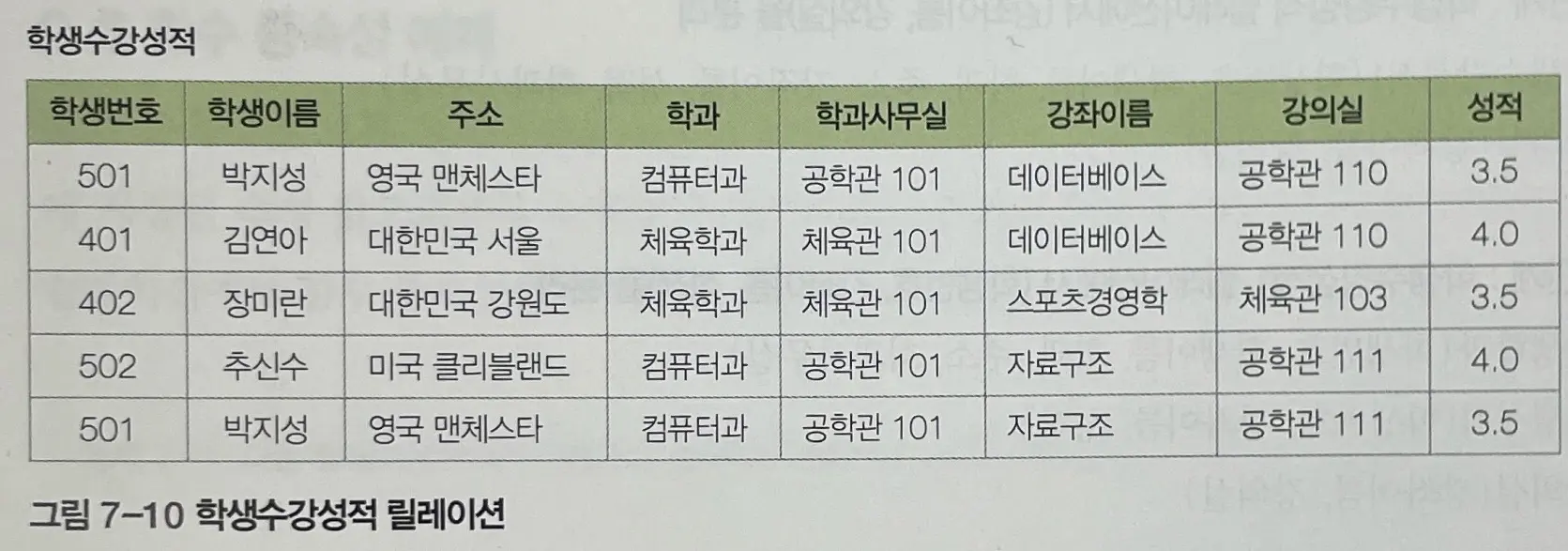
함수 종속성 테이블

학생수강성적 테이블의 기본키는 (학생번호, 강좌이름)의 복합키이다.

 

위 다이어그램을 보면 기본키가 아니면서 결정자인 속성(비후보키 결정자 속성)이 존재한다.
(학생번호, 강좌이름) -> 성적
학생번호 -> 학생이름, 학과, 주소
강좌이름 -> 강의실
학과 -> 학과사무실

 

결정자 : (학생번호, 강좌이름), 학생번호, 강좌이름, 학과

이상현상은 기본키가 아닌 결정자인 속성이 있을 때 발생한다.

 

릴레이션을 분해하기(정규화)

결정자를 기준으로 분해하면 된다.
주의할 점은, 분해시에 부분 릴레이션의 결정자는 원래 릴레이션에 남겨두어야한다.

그래야 분해된 부분 릴레이션이 원래 릴레이션과 관계를 형성할 수 있다.

 

분해 결과

 

함수 종속성은 보통 릴레이션을 설계할 때 속성의 의미로부터 정해진다.
하지만 역으로 릴레이션에 저장된 속성 값으로부터 추정할 수 있다.

 

정규화

이상현상은 두가지의 정보가 한 릴레이션에 저장되어 있기 때문에 발생한다.
따라서 이상현상은 릴레이션을 분해하여 제거한다.

분해된 릴레이션에도 이상현상이 남아있다면 이상현상이 없어질때까지 분해한다.

 

정규화 : 이상현상이 발생하는 릴레이션을 분해하여 이상현상을 없애는 과정

릴레이션을 분해하여 이상현상을 제거하는 과정

 

제 1 정규형

릴레이션 R의 모든 속성 값이 원자값을 가지면 제 1 정규형이라고 한다.

 

제 2 정규형

릴레이션의 기본키가 복합키일 때, 복합키의 일부분이 다른 속성의 결정자인지 여부를 판단하는 것이다.

제 2 정규형 : 릴레이션 R이 제 1 정규형이고, 기본키가 아닌 속성이 기본키에 완전 함수 종속일때 제 2 정규형이라고 한다.

 

완전 함수 종속

A, B가 릴레이션 R의 속성이고 A->B 종속성이 성립할 때, B가 A의 속성 전체에 함수 종속하고 부분 집합 속성에 함수 종속하지 않을 경우 완전 함수 종속이라고 한다.

 

부분 함수 종속

A->B 종속에서 A의 속성 일부를 제거해도 종속성이 여전히 성립되는 경우
ex) (A1, B1) -> B 일때 A1->B도 여전히 성립하는 경우

 

 

예시

(학생번호, 강좌이름) -> 성적
(학생번호, 강좌이름) -> 강의실
강좌이름 -> 강의실

이 때, (학생번호, 강좌이름) -> 강의실에서 학생번호를 제거해도 강좌이름-> 강의실으로 종속성이 성립한다.

 

이러한 경우 이상현상이 발생한다.

 

이상현상

• 삽입 이상 : 강좌가 개설될때 수강 신청한 학생이 없으면 NULL값으로 삽입해야한다.
• 갱신 이상 : 강의실을 변경할 경우 데이터 불일치가 발생할 수 있다.
• 삭제 이상 : 수강 취소시 강의실 정보가 사라진다.

 

제 2 정규형으로 변환

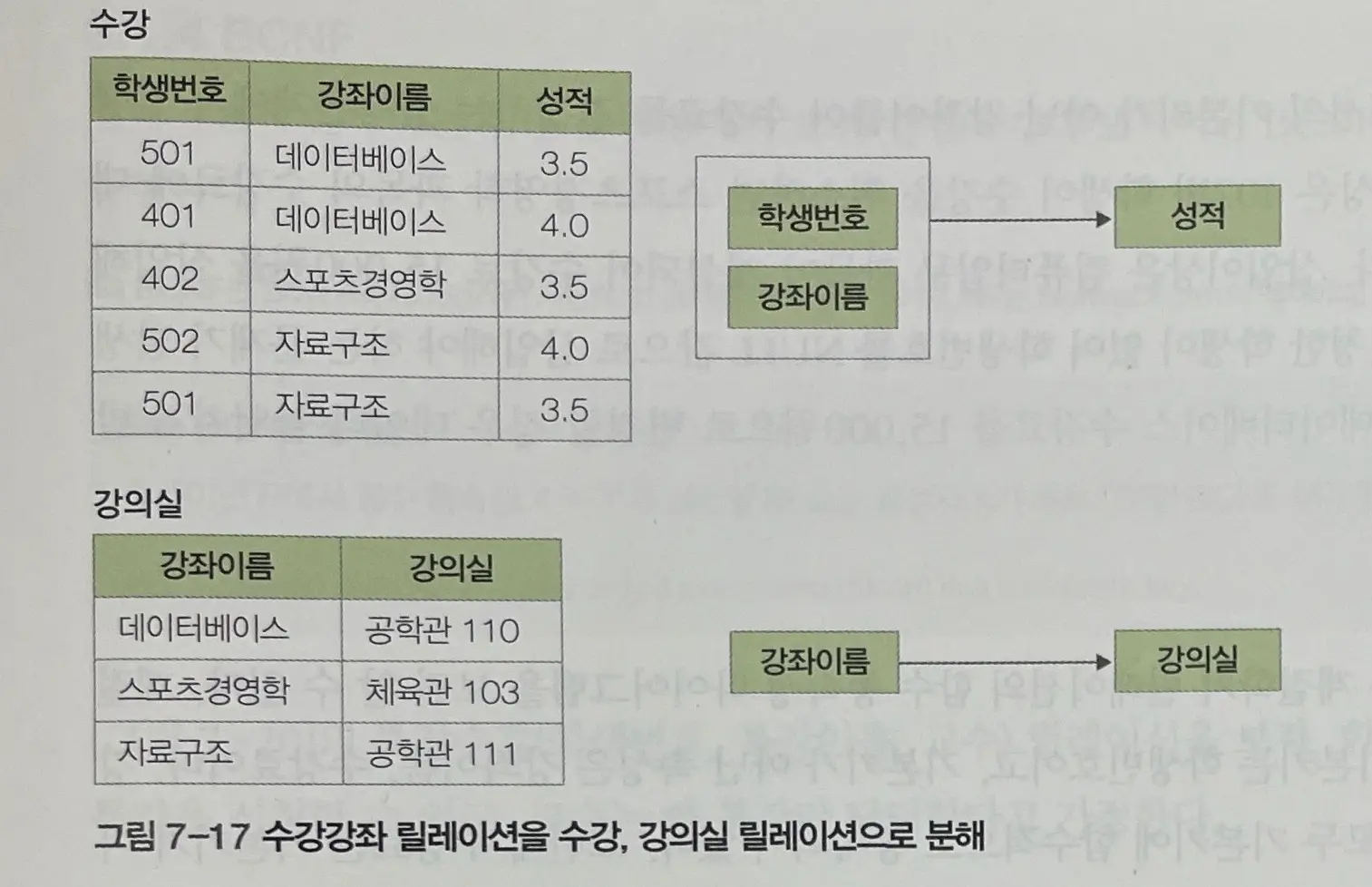
이상현상이 해결된다.

 

제 3 정규형

속성이 이행적으로 종속되어있는지 여부를 판단하는 것이다.

제 3 정규형 : 릴레이션 R이 제 2 정규형이고 기본키가 아닌 속성이 기본키에 비이행적으로 종속할 때(직접 종속) 제 3 정규형이라고 한다.

이행적 종속: A->B, B->C가 성립할 때 A->C가 성립하는 함수 종속성

제 3 정규형은 이행적 종속을 만족시키지 않도록 하는 것이다.

 

예시

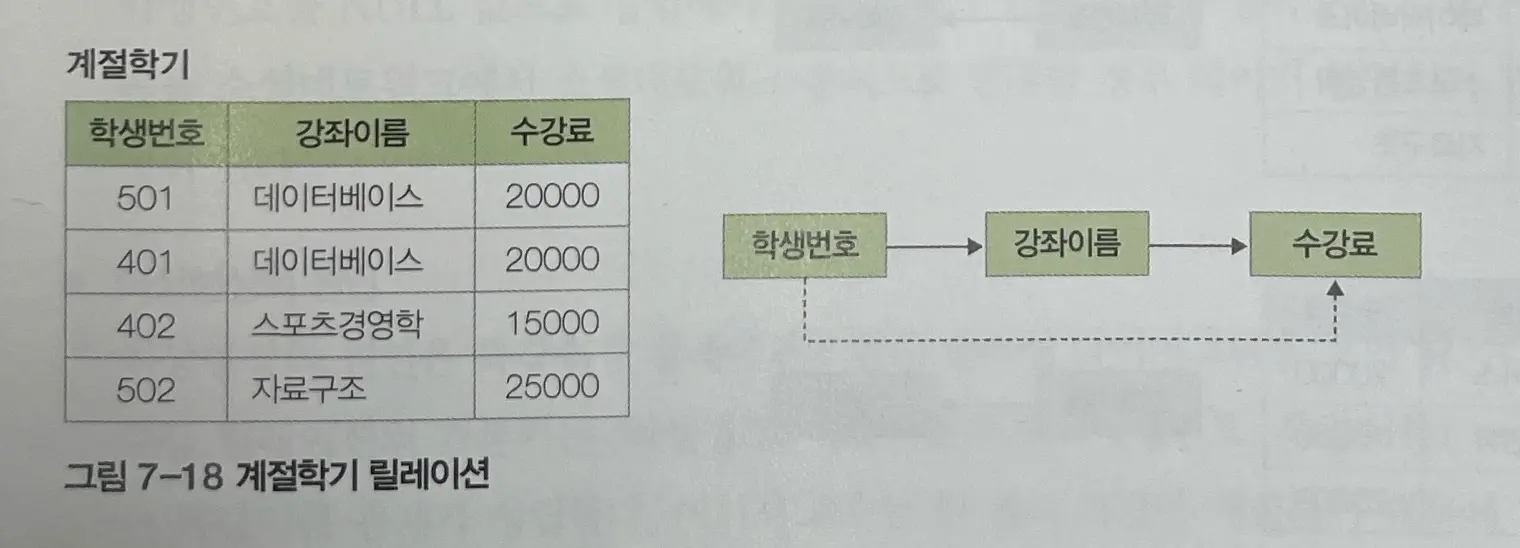
여기서 계절학기이기 때문에 학생은 하나의 강좌만 신청할 수 있다고 가정한다.

 

강좌이름과 수강료는 학생 번호에 함수적으로 종속되어 있다.
그런데 수강료는 강좌이름에 한번 더 함수적으로 종속되어 있다.

학생번호 -> 강좌이름
학생번호 -> 수강료
강좌이름 -> 수강료

수강료는 기본키에 이행적으로 종속되어 있다. (학생번호-> 강좌이름, 강좌이름 -> 수강료)

 

이상현상 발생

• 삽입 이상 : 강좌가 개설되었을 때 신청한 학생이 없다면 NULL을 삽입해야한다.
• 갱신 이상 : 수강료를 변경할 경우 데이터 불일치가 발생할 수 있다.
• 삭제 이상 : 학생이 수강을 취소할 경우 수강료 정보가 사라진다.

 

제 3 정규형으로 변환

이상현상이 해결된다.

 

BCNF

릴레이션에 존재하는 함수 종속성에서 모든 결정자가 후보키이면 BCNF 정규형이다.

BCNF 정규형 : 릴레이션 R에서 함수 종속성 X->Y가 성립할 때 모든 결정자 X가 후보키이면 BCNF 정규형이라고 한다.

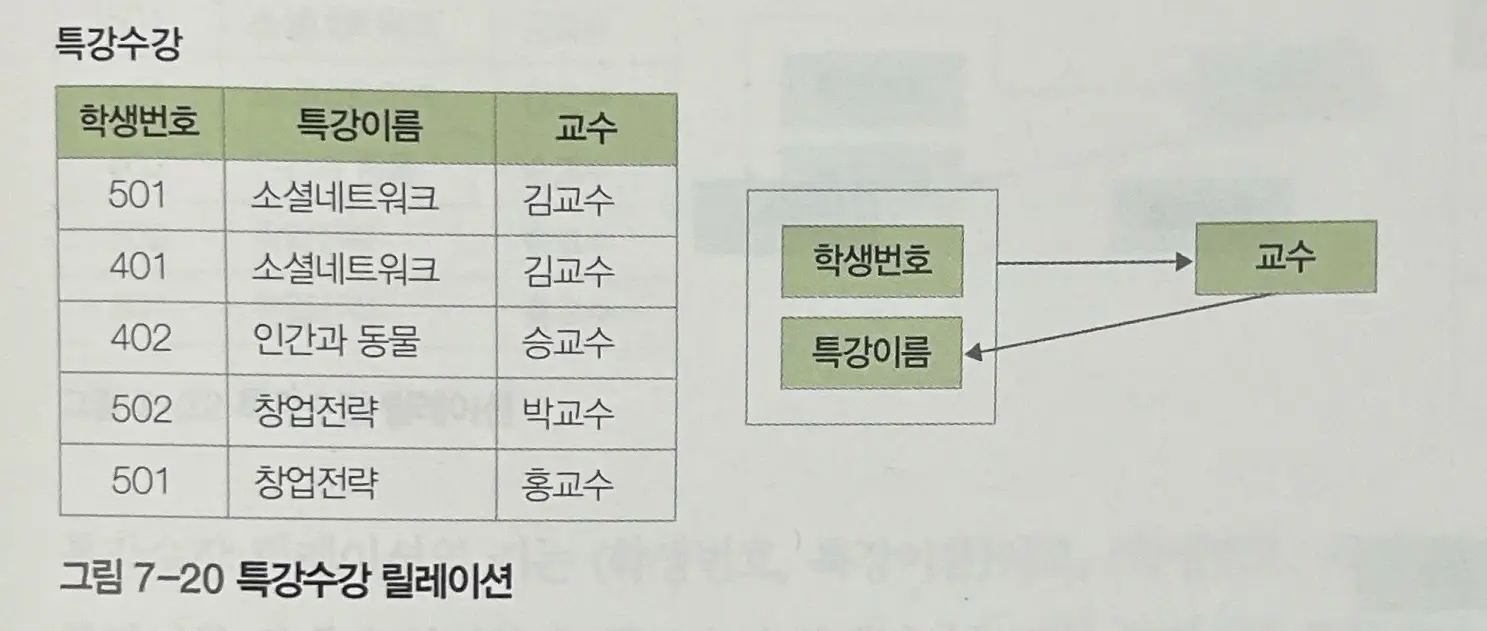
(학생번호, 특강이름) -> 교수
교수 -> 특강이름

교수는 하나의 특강만 개설한다.

 

(학생번호, 특강이름)은 후보키이지만 교수키는 후보키가 아니다.
이와 같이 결정자이면서 후보키가 아닌 속성이 존재하면 이상현상이 발생한다.

후보키 : 테이블의 모든 튜플을 유일하게 식별할 수 있는 최소 정보 (유일성, 최소성)
(학생번호, 특강이름)은 테이블 내의 모든 튜플을 유일하게 식별할 수 있어 후보키이다.
교수는 튜플을 유일하게 식별할 수 없는데, 같은 특강을 여러 교수가 개설할 수 있기 때문이다.

 

이상현상

• 삽입 이상 : 특강을 교수가 개설해도 신청한 학생이 없으면 NULL값 입력
• 갱신 이상 : 특강 이름 수정시 데이터 불일치 발생 가능
• 삭제 이상 : 학생이 수강 취소시 특강을 담당하는 교수 정보가 사라진다.

 

BCNF 정규형으로 변환

교수 식별자를 기준으로 릴레이션을 분해한다.
특강교수(교수,특강이름), 특강신청(교수, 학생번호)

학생번호와 교수는 함수적 종속관계가 아니다.

 

무손실 분해

릴레이션 분해 규칙 : 릴레이션 분해시 분해된 릴레이션간의 관계를 유지하기 위해 분해된 릴레이션에 공통 속성을 한 개 이상 두어야한다.

공통 속성은 분해된 릴레이션을 다시 원래의 릴레이션으로 조인할 때 사용한다.

 

무손실 분해란 릴레이션 R을 분해하여 두 개의 릴레이션 R1, R2를 만들었을 때 다시 조인을 하면 원래의 릴레이션 R이 만들어진다는 의미이다.

 

✅ 무손실 분해의 조건 : 분해할 때 공통된 특성(교집합)이 릴레이션 R1의 키이거나 릴레이션 R2의 키여야한다.

 

공통 속성이 릴레이션의 키가 되어야 하는 이유 => 데이터 손실 발생

예시

 

무손실 분해와 손실 분해 예시

• 공통된 속성이 한 쪽 릴레이션의 키가 되었을 때 무손실 분해 규칙을 만족하여 분해된 두 테이블을 조인하더라도 원래의 테이블이 만들어진다.

손실 분해의 경우 원래의 릴레이션에 존재하지 않는 투플이 생겨 손실(loss) 분해가 발생한다.

창업전략 관련된 2개의 투플이 더 생겼다. => 손실 발생!

 

정규화 정리

참고로 제 4 정규형은 다치 종속성을 가진 릴레이션에 관한 내용이며, 제 5 정규형은 조인종속성을 가진 릴레이션에 대한 내용이다.

 

대부분의 릴레이션은 BCNF까지 정규화하면 실제적인 이상현상은 사라진다. 따라서 보통 BCNF까지 정규화를 진행한다.

 

• 어떤 정규형 상태인 릴레이션 R1을 분해하여 만든 R2, R3 릴레이션은 R1 다음 정규형이 아닌 더 높은 정규형이 될 수 있다.
• n정규형을 만족하고 n+1 정규형을 만족시키지 못할 경우 n 정규형이다.

ex) 2정규형을 만족하고 3 정규형을 만족시키지 못할 경우 2 정규형이다.

 

Reference

책 : SQL Server로 배우는 데이터베이스 개론과 실습

https://m.yes24.com/Goods/Detail/97538787

SQL Server로 배우는 데이터베이스 개론과 실습 - 예스24